\[A = \{1, 2, 3\}\]
R reflexive irreflexive symmetric antisymmetric asymmetric transitive
\(\phi\) ❎ ✅ ✅ ✅ ✅ ✅
\(A \times A\) ✅ ❎ ✅ ❎ ❎ ✅
{(1,1),(2,2),(3,3)} ✅ ❎ ✅ ✅ ❎ ✅
{(1,2),(2,1),(1,1)} ❎ ❎ ✅ ❎ ❎ ✅
{(1,2),(2,1),(1,1),(2,2)} ❎ ❎ ✅ ❎ ❎ ✅
{(1,2),(2,3),(1,3)} ❎ ✅ ❎ ✅ ✅ ✅
{(2,3),(1,3),(1,1)} ❎ ❎ ❎ ✅ ❎ ✅
{(3,1),(1,3),(2,3)} ❎ ✅ ❎ ❎ ❎ ❎
{(2,1),(2,3),(1,1)} ❎ ❎ ❎ ✅ ❎ ✅
{(2,3),(3,2),(2,2),(3,3)} ❎ ❎ ✅ ❎ ❎ ✅
{(1,1),(2,2),(2,3),(1,3)} ❎ ❎ ❎ ✅ ❎ ✅
{(1,2),(2,1),(2,3)} ❎ ✅ ❎ ❎ ❎ ❎
{(1,1),(2,1),(1,2),(2,3)} ❎ ❎ ❎ ❎ ❎ ✅
{(1,2),(1,3)} ❎ ✅ ❎ ✅ ✅ ✅
{(2, 3)} ❎ ✅ ❎ ✅ ✅ ✅
{(1,2),(2,1)} ❎ ✅ ✅ ❎ ❎ ❎
identity: $$id_A = {(a,a)\ \ a \in A}$$

reflexive: all diagonal element must be present. \(\forall x \{x \in S \Rightarrow (x,x) \in R\}\)

irreflexive: non diagonal element can present. \(\forall x \{x \in S \Rightarrow (x,x) \not\in R\}\)

symmetric: if \((a, b) \in R\), \((b, a)\) must \(\in R\), \(a\) can \(=b\)

antisymmetric: if \((a, b) \in R\) and \((b, a) \in R\), then \(a\) must \(=b\).

asymmetric: if \((a, b) \in R\), then \((b, a) \not\in R\), even if \(a = b\).

transitive: if \((a, b) \in R\) and \((b, c) \in R\), then \((a, c)\) must \(\in R\)

Using Graph representation

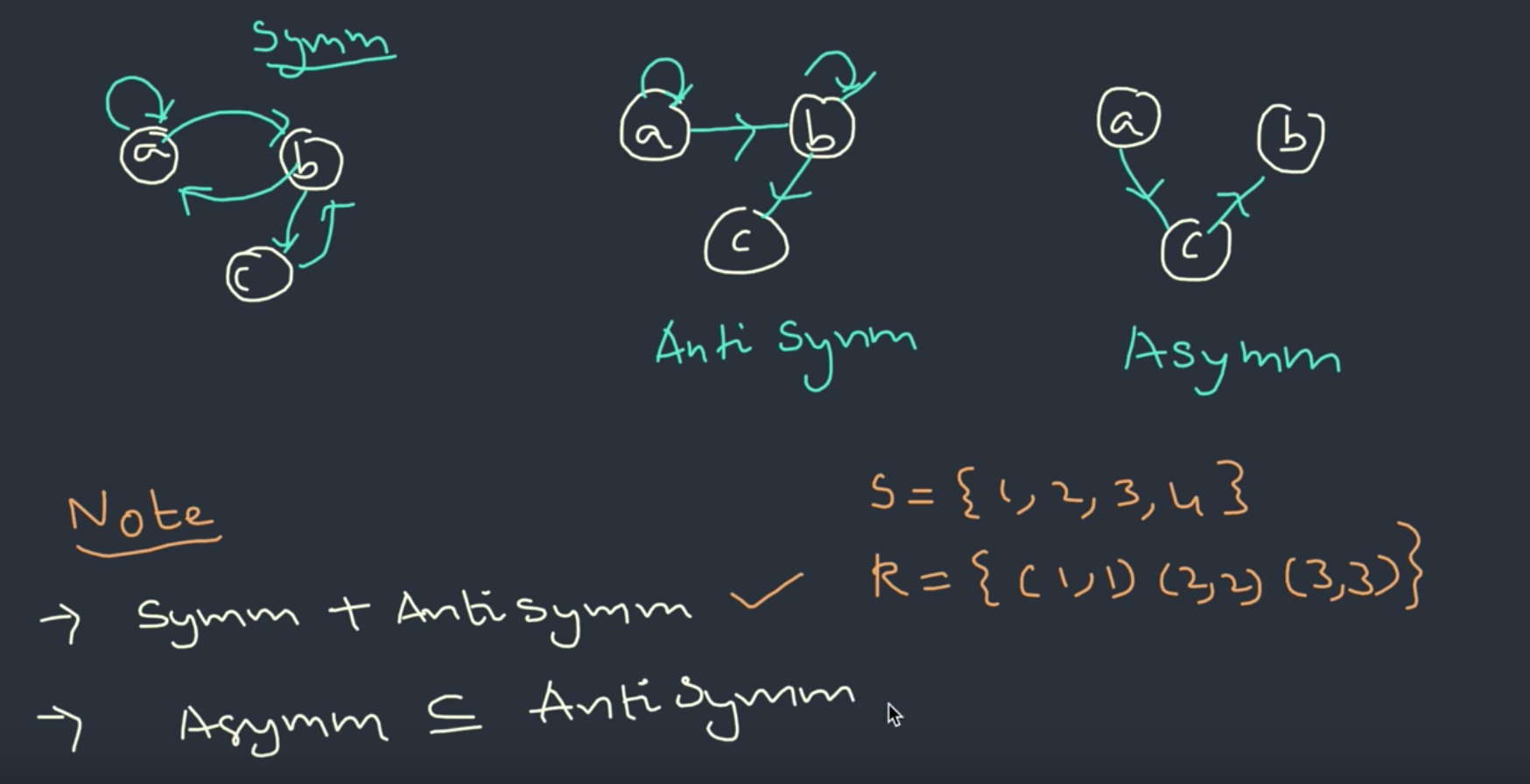
symmetric: if \(a \rightarrow b\), then must have \(b \rightarrow a\), \(a \rightarrow a\) is permitted.

antisymmetric: if \(a \rightarrow b\), then must not have \(b \rightarrow a\), \(a \rightarrow a\) is permitted.

asymmetric: if \(a \rightarrow b\), then must not have \(b \rightarrow a\), \(a \rightarrow a\) is not permitted.

asymmetric \(\subseteq\) antisymmetric